Trong một vùng đất xa xôi của các con số, nơi mà mỗi con số được xem như một số hiệu của nốt nhạc mang âm sắc riêng biệt, tồn tại một giai điệu đặc biệt gọi là "hài hòa". Người dân vùng đất ấy tin rằng, một dãy số chỉ thật sự trở nên đẹp và đầy cảm hứng khi các số hiệu nốt nhạc trong đó hòa quyện với nhau theo một quy luật tinh tế: khoảng cách giữa nốt cao nhất và nốt thấp nhất phải đúng bằng ~1~. Chính giai điệu ấy đã tạo nên "bản giao hưởng số hài hòa" vốn mang đến cảm giác nhẹ nhàng và tràn đầy sức sống.

Nhiệm vụ của bạn, với vai trò là một nhạc sĩ tài ba của vương quốc số học, là phải chọn ra một số nốt nhạc sao cho tạo thành "đoạn nhạc" dài nhất trong một dãy nốt nhạc cho trước, sao cho đoạn nhạc đó vẫn giữ được sự "hài hòa" - nghĩa là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất trong đoạn chỉ bằng đúng ~1~. Qua đó, bạn sẽ mở ra những giai điệu mới, giúp những con số tỏa sáng trong vũ khúc rộn rã của chúng.

Input

• Dòng đầu: Gồm một số nguyên dương ~n~ là số lượng nốt nhạc. ~(n \leq 10^6)~
• Dòng tiếp theo: Gồm ~n~ số nguyên dương lần lượt là các số hiệu của nốt nhạc có giá trị không vượt quá ~10^6~.

Output

• Gồm một số nguyên duy nhất là độ dài đoạn nhạc lớn nhất tìm được.

Sample Input

10
1 3 2 2 5 2 9 7 2004 3

Sample Output

5

Constraints

• ~40\%~ số test đầu tiên tương ứng với ~40\%~ số điểm có ~n \leq 20~.
• ~30\%~ số test tiếp theo tương ứng với ~30\%~ số điểm có ~n \leq 10^4~
• ~30\%~ số test cuối cùng tương ứng với ~30\%~ không có ràng buộc gì thêm.

Ở một thời xa xưa, trong vùng đất của những bí ẩn và truyền thuyết, có một vương quốc nơi mà các chữ cái không chỉ đơn thuần là những ký hiệu mà còn chứa đựng sức mạnh của tri thức và sự sáng tạo. Người dân vùng đất ấy tin rằng, mọi thông điệp quan trọng đều được ẩn giấu dưới dạng các chuỗi ký tự - những bức tranh tinh vi được xây dựng từ một mảnh ghép nhỏ lặp đi lặp lại nhiều lần theo một mẫu số bí ẩn.

Hôm nay, bạn được giao cho nhiệm vụ đặc biệt: mở khóa bí mật của một thông điệp cổ xưa. Bạn cần phải kiểm tra xem những chuỗi ký tự ~s~ được đưa ra có thể "sống" bằng cách lặp đi lặp lại một mẫu con nào đó không. Nếu có, điều đó đồng nghĩa với việc thông điệp ấy được xây dựng trên nền tảng của một cấu trúc lặp lại, một dấu hiệu cho thấy thông điệp này chứa đựng thông tin quý giá của một nền văn minh cổ xưa.

Input

• Dòng đầu: Gồm một số nguyên dương ~T~ là số lượng xâu. ~(T \leq 100)~
• ~T~ dòng tiếp theo: Mỗi dòng một xâu ~s~ có độ dài không vượt quá ~10^5~.
• Tổng độ dài các xâu ~s~ đã cho có giá trị không vượt quá ~10^6~.

Output

• Gồm ~T~ dòng, với mỗi dòng in ra true nếu thông điệp được xây dựng theo cấu trúc lặp lại, ngược lại in ra false.

Sample Input

4
abab
aba
abcabcabcabc 
abba

Sample Output

true
false
true
false

Constraints

• ~30\%~ số test đầu tiên tương ứng với ~30\%~ số điểm có ~|s| \leq 10^2~.
• ~40\%~ số test tiếp theo tương ứng với ~40\%~ số điểm có ~|s| \leq 10^4~
• ~30\%~ số test cuối cùng tương ứng với ~30\%~ không có ràng buộc gì thêm.

Trong một vương quốc xa xôi, nơi những con số không chỉ tồn tại để đếm và tính toán, mà còn mang trong mình những tính cách và sứ mệnh bí ẩn, có một truyền thuyết kể về "Sự Diêu Hóa của Số". Theo truyền thuyết này, mỗi con số trong vương quốc đều có khả năng biến đổi năng lượng, và khi chúng gặp nhau theo một trật tự nhất định, một phép màu lại được tạo ra.

Người xưa kể rằng, có một tập hợp những con số đặc biệt đôi một khác nhau, được gọi là ~A~ có độ dài ~m~. Đó là những con số được sắp xếp theo một trật tự riêng biệt, nơi mỗi con số có khả năng "gọi mời" con số lớn hơn nằm bên phải nó - được gọi là "phần tử lớn hơn kế tiếp". Tuy nhiên, không phải lúc nào lời mời ấy cũng thành công; có những con số, dù cố gắng, lại chẳng thể tìm thấy người bạn đồng hành phù hợp, và chúng buộc phải đứng một mình giữa dòng chảy của các con số.

Thêm phần ly kỳ hơn, tồn tại thêm một tập hợp nhỏ hơn, mang tên ~B~ có độ dài ~n~, được chọn lọc ra từ ~A~ (có thể chọn một số trong tập hợp ~A~ nhiều lần). Những con số trong ~B~ đều là những "nhân vật chính" của câu chuyện, và sứ mệnh của chúng là tìm kiếm người bạn "lớn hơn kế tiếp" của chính mình trong vương quốc rộng lớn của ~A~.

Nhiệm Vụ Của Người Hùng: Với vai trò là một chiến binh trí tuệ, bạn được giao nhiệm vụ giải mã bí ẩn của "phần tử lớn hơn kế tiếp" theo cách sau:

• Xác định vị trí của mỗi nhân vật:
  • Với mỗi con số ~x~ trong ~B~ (với chỉ số từ ~1~ đến ~n~), tìm vị trí của nó trong tập hợp ~A~.
• Khám phá lời mời của các số:
  • Sau khi xác định được vị trí của ~x~ trong ~A~, hãy tìm phần tử đầu tiên bên phải của ~x~ mà có giá trị lớn hơn ~x~. Đây chính là người bạn "lớn hơn kế tiếp" của ~x~ trong vương quốc của các con số.
• Phép màu của sự biến hóa:
  • Nếu tồn tại một con số như vậy, ghi nhận nó như là kết quả của ~x~.
  • Nếu không tìm được, ghi nhận rằng ~x~ không tìm thấy người bạn đồng hành phù hợp và trả về giá trị ~-1~.
• Bộ sưu tập kết quả:
  • Cuối cùng, bạn cần xây dựng một danh sách với độ dài bằng ~n~, sao cho phần tử thứ ~i~ chứa phần tử "lớn hơn kế tiếp" của ~B_i~, hay là ~-1~ nếu không có.

Input

• Dòng đầu: Gồm một hai số nguyên dương ~m~ và ~n~. ~(m, n \leq 10^6)~
• Dòng thứ hai: Gồm ~m~ số nguyên dương ~A_i~ có giá trị không vượt quá ~10^9~.
• Dòng cuối cùng: Gồm ~n~ số nguyên dương ~B_i~ được chọn lọc ra từ ~A~.

Output

• Một dòng duy nhất là danh sách gồm ~n~ số nguyên được cách nhau bởi khoảng trắng.

Sample Input

4 3
1 3 4 2
4 1 2

Sample Output

-1 3 -1

Explanation

• Với con số ~4~, tìm được tại vị trí thứ ~3~: không có con số nào bên phải có giá trị lớn hơn ~4~, nên kết quả là ~-1~.
• Với con số ~1~, tìm được tại vị trí thứ ~1~: con số đầu tiên bên phải có giá trị lớn hơn là ~3~, nên kết quả là ~3~.
• Với con số ~2~, tìm được tại vị trí thứ ~4~: không có con số nào bên phải, nên kết quả là ~-1~.

Constraints

• ~60\%~ số test đầu tiên tương ứng với ~60\%~ số điểm có ~m, n \leq 5 \times 10^3~.
• ~40\%~ số test cuối cùng tương ứng với ~40\%~ số điểm không có ràng buộc gì thêm.

Trong một chiến dịch quy mô lớn của Liên minh Không gian, bạn được giao nhiệm vụ thiết lập hệ thống truyền tín hiệu điều khiển từ Trạm Trung Tâm được đánh số thứ tự là ~1~ đến toàn bộ các trạm vệ tinh còn lại (từ ~2~ đến ~n~). Các tín hiệu sẽ được truyền qua các vệ tinh trung gian, thông qua những tuyến truyền có sẵn.

Mỗi tuyến truyền là một kết nối một chiều từ vệ tinh ~u~ đến vệ tinh ~v~, với một mức nhiễu tín hiệu là ~w~. Nếu tín hiệu đi qua tuyến này, nó sẽ chịu ảnh hưởng bởi độ nhiễu ~w~, có thể làm sai lệch mệnh lệnh điều khiển.

Tuy nhiên, không phải tuyến nào cũng cần được sử dụng. Bạn có thể tắt bớt một số tuyến truyền, với điều kiện là vẫn phải đảm bảo mọi trạm vệ tinh đều có thể nhận tín hiệu khởi nguồn từ Trạm Trung Tâm.

Mục tiêu của bạn là thiết kế lại hệ thống sao cho:

• Mỗi trạm vẫn nhận được tín hiệu từ trạm trung tâm.
• Trong toàn bộ hệ thống được giữ lại, tuyến truyền nào có mức nhiễu cao nhất thì mức nhiễu đó phải nhỏ nhất có thể. Nói cách khác, hãy giảm tối đa ảnh hưởng của nhiễu tồi tệ nhất có thể xảy ra trong bất kỳ tuyến truyền nào được giữ lại.

Input

• Dòng đầu: Chứa hai số nguyên dương ~n~ và ~m~ lần lượt là số trạm vệ tinh và số tuyến truyền tín hiệu.
• ~m~ dòng sau: Mỗi dòng gồm ba số nguyên dương ~u,v~ và ~w~ thể hiện tuyến truyền tín hiệu một chiều từ trạm ~u~ đến trạm ~v~ có độ nhiễu là ~w~. ~(w \leq 10^9)~

Output

• Gồm một số nguyên duy nhất là đáp án của nhiệm vụ đã giao hoặc in ~-1~ nếu không có đáp án thoả mãn.

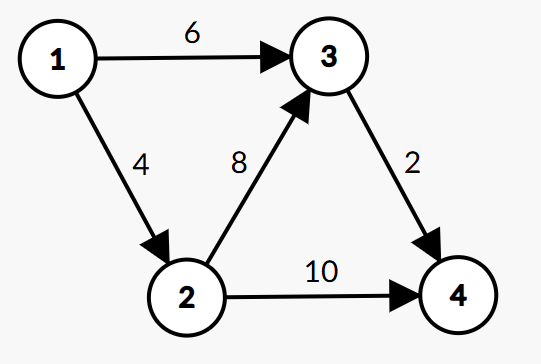
Sample Input

4 5
1 2 4
2 3 8
1 3 6
3 4 2
2 4 10

Sample Output

6

Explanation

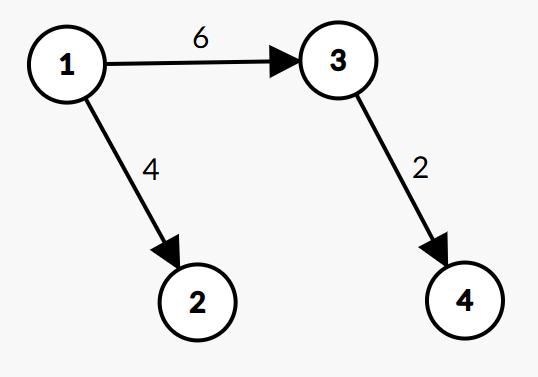
• Loại bỏ tuyến truyền tín hiệu ~2 → 3~ có trọng số là ~8~ và tuyến truyền tín hiệu ~2 → 4~ có trọng số là ~10~.
  • 
• Sau khi hoàn thành nhiệm vụ thiết lập hệ thống truyền tín hiệu điều khiển từ Trạm Trung Tâm:
  • 

Constraints

• ~40\%~ số test đầu tiên tương ứng với ~40\%~ số điểm có ~n \leq 100, m \leq 10^3~.
• ~20\%~ số test tiếp thep tương ứng với ~20\%~ số điểm có ~n \leq 10^3, m \leq 10^4~.
• ~20\%~ số test tiếp theo tương ứng với ~20\%~ số điểm có ~n \leq 10^4, m \leq 10^5~.
• ~20\%~ số test cuối cùng tương ứng với ~20\%~ số điểm có ~n \leq 10^5, m \leq 5\times10^5~.